A Test for Maximal Winnings
What’s the ideal number of tickets to buy? This question has vexed me for years.
There must be a number that maximizes potential returns from scratcher prizes that also limits losses. That number could even allow you to propel your occasional prize winnings forward to more scratchers.
Buying too many tickets results in losing money to diminishing returns. Yet, buy too few and you may not win enough prizes. Either way, you never win enough cash to overcome the amount you spend buying scratchers.
I’ve recommended buying a cluster of scratchers equal to that of three standard deviations from the average odds of winning prizes. This would use the 68-95-99.7 rule and avoid diminishing returns. So if the average odds is 4 to 1 (one prize for every four scratcher tickets) then the number of scratchers might be 9 or as many as 12, depending on how large the standard deviation. In that cluster would be at least one winning scratch-off. But would you win enough prizes to make up for the cost?
Finally, I decided: let’s just test it. Get scratchers in clusters, and see how many return a profit in the end.
“Buy” Enough Scratchers to Find Out if the Strategy Works
Unfortunately, I don’t have the cash to do a true statistical test.
To separate what’s statistically true from what’s just luck, you’ve got to buy enough scratchers for a large enough sample. For the millions of scratchers issued, that means over 1,000 tickets for each game for a sample that would have a small margin of error (+/- 3%) and a high level of confidence (95%). That would have required spending millions for each game only to lose millions for most games.
But I could conduct a simulation. I could do that in a fraction of the time it would take to buy all the real tickets I would have needed. Create arrays of tickets, randomly select “tickets,” and see how many turn up winners. Then see if the amount of winnings overcome the amount that would have been spent.
I wrote some code in Python to:
- Create an array to serve as a “pool” of all scratcher tickets – including all prizes – still unclaimed, as posted on VaLottery.com.
- Calculate the number of tickets needed for a statistically significant number of tickets, based the total tickets still available.
- Create an array that serves as a “roll” of scratchers, and fill that array by randomly selecting a “ticket” from the large pool of scratchers. Whether this was a winner depended on the actual prize probabilities.
- Select a cluster of tickets, starting at a randomly selected number in a “roll” of tickets (based on the actual roll sizes by game cost, based on the retailer manual). This way, the tickets would be “bought” just like if you walked into 7-Eleven and started buying them with zero idea of how many tickets from that roll had been bought before you.
- Add each cluster to a running list of clusters, summing up the total wins and loses.
- Calculate the number of “observed winners” and statistically compare that with the current probabilities.

With this code, I could run this simulation to test the impact by various amounts of cluster sizes.
I ran this simulation for a statistically significant sample size of scratchers for each game. Furthermore, I ran this simulation for each game using different cluster sizes. The cluster sizes varied depending on the number of standard deviations, ranging from three below the average probability of winning a prize to three above the probability of winning. I ran these simulations based on data posted by the Virginia Lottery on March 8, 2022.
I ultimately ran seven trials for each scratcher game – one for each standard deviation from three below the mean to three above the mean, including once for the mean itself. This means that each trial involved simulating the ticket outcomes of an average 1,100 tickets per game, in 200+ clusters that ranged in size from one to 181.
Further-furthermore, I did it all over again based on the number of standard deviations from the probability of winning a prize that returns a profit over the cost of scratcher – a “profit prize.” So I ran a total of 1,177 trials.
As it turned out from my experiment, conducting this test in reality would have required spending as much as $11.2 million only to lose as much as $10.9 million. Of course, most games resulted in a loss.

Yet, some games actually returned not only a profit, even as much as hundreds of thousands of dollars. For one game, the $5 Monopoly Fortunes game actually resulted in over $1 million – though for me it was just Monopoly money.
The Results – Some Scratcher Games Returned More Prizes than Expected
Once I had the final results in hand, I tested whether the “observed” prize frequency (i.e., The number of “prizes won” divided by the number of “tickets bought”) was consistent with the actual probability, based on the data provided on the official Virginia Lottery website.
For 27% of trials (315 trials), the number of prizes was exactly within the expected range of prizes based on the data posted on VALottery.com. A two-way Z-test, by calculating a Z-score from the proportions, confirmed as much. For these trials, the observed percent of prizes “won” was within a statistically expected range of the known probability, and as the p-value was below 0.05 I had to accept the null hypothesis, i.e., that the observed win rate was statistically the same as the expected win rate.
That’s a wonky statistician’s way of saying that I got as many prizes as I expected, regardless of how large or small the number of tickets in each cluster. On average, the proportion of tickets with a prize that I observed was 24% while the number of scratcher tickets that had a prize was also 24%. I did come out with more money in prizes after 20 of these trials, but my average total prize winnings was a loss of $8,545.
Another 37% of trials (438 trials) returned worse results than expected – there were fewer winning tickets than expected. The observed frequency of prize-winning tickets was 19%, while the average prize probability was 25%. In these trials, I came out ahead in just 12 trials and my final average tally was a negative $17,879.
Okay, so 1 out of 4 results were as expected, and another 2 out of 5 results were worse than expected. But that’s the boring part – the “expected” results aren’t all that exciting, are they? And there’s nothing exciting about winning the same or less than expected.
The exciting part is: when did I get a higher win rate than expected? Believe it or not, that happened. For 36% of trials (423 trials), I landed a statistically significant higher number of winning scratchers than the expected average. I observed an overage 32% of tickets had a prize, over the average expected 25% probability. My average tally was still negative, albeit a smaller average loss of $835.
However, I came out ahead in far more games in trials where the win rate was statistically higher than average. For 83 trials, I won more than I spent on scratchers; the final tally was on average $28,349 – boosted by high earnings that for some games totaled over hundreds of thousands.
The Best Number of Scratchers to Buy
“Okay, so how’d that happen?” you might be asking. Well, it all depends on the size of the clusters.
The question was always: how many tickets do I really need to buy? What’s the sweet spot between spending too much money on tickets and spending too little to win anything significant?
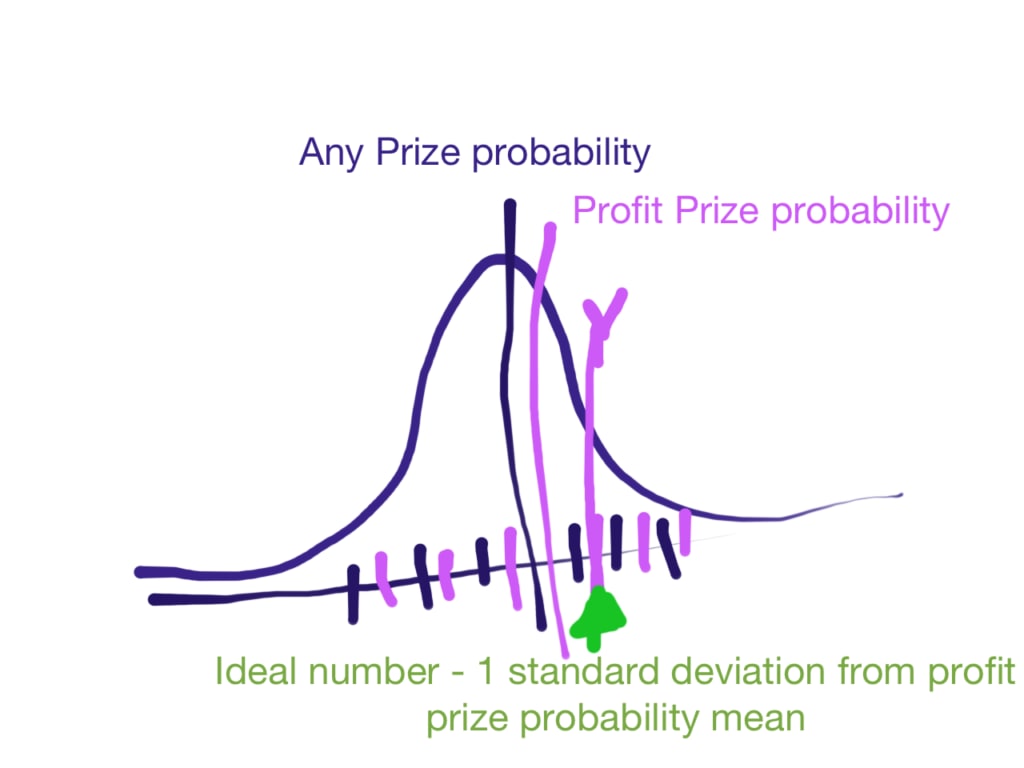
I narrowed down the cluster sizes that resulted in positive outcomes most often. But remember that the cluster size varied by the number of standard deviations from the mean prize probability. In my simulation, the cluster size corresponding to one standard deviation from the mean probability of a “profit prize” is the ideal number. This means that in general the number of scratcher tickets you’ll buy ranges from 5 to 12, an average of 8 tickets.
In past articles, I’d recommended a strategy that was three standard deviations from the profit prize mean, a range of 7 to 28, an average of 16. As it turned out, that was too many. You only need to buy half as many scratchers on average for the best odds.
You can find the raw data here to see for yourself:
In that file you can find data on:
- The number of games with a positive final tally
- Number of games with a high z-score
- Games with an observed frequency higher than the probability
- Games with a higher average cluster outcome
Based on this data, I’ve gone back and revised my initial recommendation to buy based on three standard deviations from the mean. Turns out, you’re spending too much money doing that. This is good news – you can spend less to win more!
NOTE: Please remember that while I did this test based on real data, the results are only hypothetical. I could do the same test with same data and the results may differ.

